Link identifier archive #link-archive-thumb-soap-44415
Nell'ambito dei Tè di Matematica, mercoledì 4 giugno alle ore 16:00, Margarida Melo (Università Roma Tre) terrà un seminario dal titolo "Tropicalizing curves and divisors".
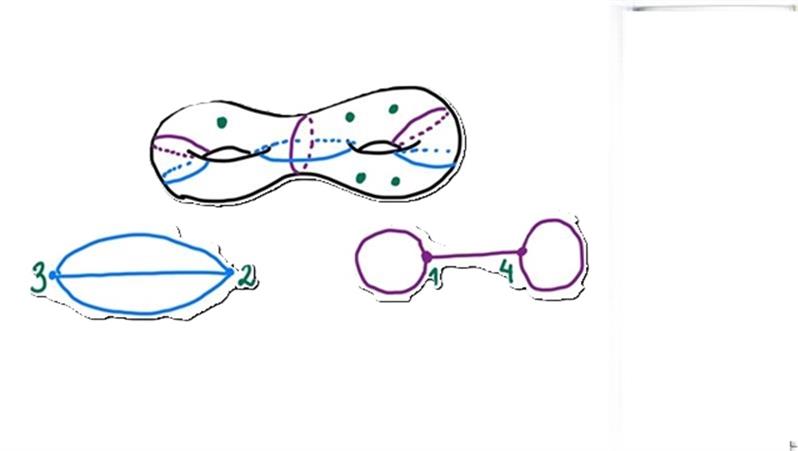
Abstract: In algebraic geometry, understanding the geometry of degenerations of fundamental objects as curves is of central importance in the study of the initial objects themselves. However, dealing with degenerated objects is often hard from the point of view of the combinatorial data one has to handle. In the last few years, a very sucessful approach to handle degeneration data has been to use tools from tropical geometry. Indeed, it is often the case that by tropicalizing algebro-geometric objects, one gets a modular way to describe degeneration data, which can then be treated as moduli spaces themselves. This interplay between degenerated algebro-geometric objects and their tropical counterparts has led to incredible developments in our current understanding of the geometry of both. In the talk, I will try to explain these ideas in the case of curves and divisors on curves. In particular, I will illustrate the tropical version of the Rieman-Roch theorem and how to use specialization techniques to prove a number of results in classical algebraic geometry via their tropical/combinatorial counterparts.
Il seminario si svolgerà in presenza presso il Dipartimento di Matematica e Fisica, Lungotevere Dante 476, aula M3.
